Сетевой График Строительства Пример
Он представляет собой сетевую модель с рассчитанными временными параметрами, использующими в качестве основных элементов работу и событие, а также ожидание, зависимость, путь, критический путь и др. Работа - это производственный процесс, требующий затрат труда, времени и материально-технических ресурсов и приводящий к достижению определенных результатов (например, рытье траншеи или котлована, монтаж труб или конструкций сооружений и т.
Работу на сетевом графике изображают сплошной стрелкой, длина которой не обязательно должна соответствовать продолжительности работы, особенно если график строится не в масштабе времени. Над стрелкой указывают наименование работы, а под ней ее продолжительность. Событие - это факт окончания одной или нескольких работ, необходимый и достаточный для начала последующих работ. Таким образом, события определяют технологическую и организационную последовательность работ. Событие обозначают геометрическими фигурами (кружками, квадратами и т. И.) с цифровым кодом внутри. Между двумя событиями может выполняться только одна работа, но к каждому событию может примыкать одна или несколько оканчивающихся работ (рис.

Смежные два события ограничивают данную работу и по отношению к ней могут быть начальными и конечными (рис. Начальное событие і определяет начало данной работы и является конечным для предшествующих работ. Конечное событие j - окончание данной работы и является начальным для последующих работ. Исходное событие И - начало выполнения всех работ по строительству объекта. Оно не имеет предшествующих работ, т. В него не входит ни одна работа.
Завершающее событие к - достижение конечной цели, оно не имеет последующих работ в рамках рассматриваемого сетевого графика, т. Из него не следует ни одна работа. Ожидание - это процесс, не требующий никаких ресурсов, а только затрат времени (например, твердение бетона, сушка штукатурки, окраски и т. Поэтому ожидание является технологическим или организационным перерывом между работами, выполняемыми непосредственно друг за другом. Ожидание, как и работа, графически изображается сплошной стрелкой. Зависимость - фиктивная работа, которая вводится для отражения технологической и организационной взаимосвязи работ и не требует ни времени, ни ресурсов. В сетевом графике зависимость обозначается пунктирной стрелкой и при его построении указывает зависимость начала одной работы от окончания другой.
Пример использования зависимости показан на сетевом графике устройства подземной части здания (рис. Путь - непрерывная последовательность работ в сетевом графике. Его длина определяется суммой продолжительности входящих Рис.
- Поэтому сетевой график «перекочевал» из строительства практически во все отрасли. Итак, что же отображается в этом документе? Во-первых, подробнейшим образом перечисляются все операции, необходимые для выпуска товаров (производства услуг).. Разработанный сетевой график (пример построения его приведен на рисунке) передается на производство и воплощается в жизнь. Но что стоит за цифрами и расчетами? Как использовать возможные технологические простои или, наоборот, избежать форс-мажорных ситуаций.
- Вершины графа отображают состояния некоторого объекта (например, строительства), а дуги — работы, ведущиеся на этом объекте. Вершины графа отражают работы, а связи между ними — зависимости между работами. Правила построения сетевого граифка.. На рисунке 1 показан пример начала сетевого графика с одной исходной работой (работа A), а на рисунке 2 пример начала сетевого графика с тремя исходными работами (работы A, B, C). Сетевой график с одной исходной работой. Сетевой график с тремя исходными работами. Последовательные работы.
2) сетевой график строительства объекта в масштабе времени с построением. При составлении сетевого графика. Которое не вызовет задержки окончания строительства.
Обозначения элементов сетевого графика в него работ. Между исходным и завершающим событием в сетевом графике может быть несколько путей и каждый из них называется полным. Участок полного пути, от данного события до исходного, называется предшествующим, а от него до любого последующего - последующим.
Приведенный на рис. 8.2, г сетевой график устройства подземной части здания имеет четыре полных пути с разной продолжительностью: Критическим путем называют один или несколько полных путей сетевого графика, имеющих наибольшую продолжительность (длину). На приведенном графике критический путь № 3 проходит через события 1-2-5-7-8 продолжительностью в 21 день. Другие пути располагают некоторым запасом (резервом) времени. Например, путь № 2 имеет запас времени в 3 дня (21 - 18), а путь № 4 - 5 дней (21-16). Близкие по продолжительности пути к критическому называют подкритическими, а остальные - некритическими, их увязывают с периодичностью контроля хода строительства.
Длина критического пути определяет общий срок строительства объекта по сетевому графику. Работы, лежащие на критическом пути, называют критическими, и в случае затягивания их выполнения произойдет общее удлинение сроков всего строительства по данному графику. Поэтому для сокращения общей продолжительности строительства необходимо прежде всего ускорять критические работы. Критический путь на графике выделяется утолщенной или двойной линией. Если основой сетевого метода является график производственного процесса, то основной составляющей частью сетевой модели, выражающей один производственный процесс (работу), - вектор в виде стрелки.
Таким образом, сетевой график представляет собой стрелочную диаграмму, состоящую из работ и событий. Стрелки на графике изображаются не в масштабе, их можно чертить в виде прямой или ломаной линии, но прерывать нельзя.
Стрелки в сетевом графике располагаются в порядке, который характеризует логическую последовательность выполнения работ. При этом очень важно решить: какая работа предшествует данной работе, какая работа сопутствует данной работе, какая работа следует за ней. Полученные в результате решения этих вопросов сочетания стрелок и образуют сетевой график. Разновидности сетевых графиков. В зависимости от способа изображения работ на сетевом графике различают сети типа «работы- вершины» и «работы-дуги».
В зависимости от содержания информации о составе и параметрах работ графики подразделяются на детерминированные и альтернативные (вероятностные), а в зависимости от числа технологических комплексов работ, отражаемых в модели, - на одно- и многосетевые. В свою очередь односетевые модели в зависимости от достижения конкретных результатов могут быть одно- и многоцелевыми. Многосетевые модели всегда многоцелевые. По составу параметров различают сетевые модели с учетом времени, стоимости и ресурсов. Сетевые модели с учетом времени подразделяются на несколько следующих классов: ПВД - это простейшая детерминированная временная; ДВ - детерминированная временная; ОДВ - обобщенная детерминированная временная; ВВ(д) - вероятностная временная с детерминированной сетью; ВВ(а) - вероятностная временная с альтернативной сетью. Сетевые модели с учетом стоимости подразделяются на линейные и нелинейные, а с учетом ресурсов - на модели с учетом потребностей в ресурсах и с распределением ресурсов. Правила построения сетевых графиков.
Для правильного отражения взаимосвязи между работами сетевого графика необходимо при его построении соблюдать ряд правил. Направление стрелок в сетевом графике принимают слева направо.
Форма графика должна быть простой, график не должен иметь лишних пересечений, работы в основном следует изображать горизонтальными линиями. Если работы выполняются последовательно, то на графике их изображают следующими одна за другой (см. Если результат работы А необходим для выполнения работ Б и В, то на сетевом графике это изображают, как показано на рис. 8.3, а, и наоборот, если результат работ А и Б является необходимым условием для начала работы В, то пример правильного изображения этого показан на рис. Правила построения сетевого графика (1) 5. При параллельном выполнении работ, т.
Когда одно событие служит началом двух или большего числа работ, заканчивающихся другим событием (рис. 8.3, в), для недопущения одинакового обозначения (кодирования) разных работ при построении графика вводят зависимости (фиктивные работы) и дополнительные события (рис. Если работы (например, Б, В и Г) могут быть начаты после частичного выполнения работы А, то последнюю следует разбить на части (участки) Ар А2, А3.
Ая и каждая часть на графике будет считаться самостоятельной работой (рис. При расчленении работы на участки (захватки) на сетевом графике ее можно представить как сумму последовательно выполняемых работ (рис. Если две какие-либо работы В и Е непосредственно зависят от совокупного результата двух других работ А и Б, то такую зависимость изображают, как показано на рис. Если для начала работы В необходимо выполнить предшествующие работы А и Б, а для начала работы Е выполнить только работу А, в такой график вводят зависимость (фиктивную работу) 3-4 (рис. Если после завершения работы А можно начать работу Е, а начало работы Д зависит от завершения работ А и Б, в сетевой график вводят две зависимости 3-5 и 4-5 (рис.
Сетевой график не должен иметь замкнутых контуров (циклов), т. Цепочки работ, возвращающейся к тому событию, из которого она вышла (рис. Если такие контуры возникли при построении графика, то это свидетельствует об ошибке планирования, и чтобы ее исправить, нужно променять направления стрелок работы 2-6 на рис 8.4, а и работы 2-4 на рис 8.4, б. В одноцелевом сетевом графике не должно быть «тупиков» (3-4), т. Событий (4), которые не являются началом других, последующих работ (рис. Не должно быть также «хвостов» (2-3), которые не являются результатом каких-либо предшествующих работ, и «висячих» событий (2), в которые не входит ни одна работа (рис 8.4, г).
Исключением являются исходное и завершающее события сетевого графика. Наличие в сети «тупиков» и «хвостов» с «висячими» событиями свидетельствует об ошибке или о том, что эту работу выполнять никому не поручено. Поэтому нужно найти исполнителя и включить работы с «висячими» событиями в сеть. В сетевом графике не должно быть лишних событий (рис. А в случае их обнаружения график надо перестроить, как показано на рис.
8.4, е, так как одна работа не может связывать более двух событий. Правила построения сетевого графика (2) 13. При необходимости отражения на сетевом графике поточной организации работ особое внимание необходимо уделить правильной разбивке работ на захватки и выявлению взаимосвязи смежных работ. При этом на горизонтальном участке сетевого графика можно показывать или однородные работы по всем захваткам, или весь комплекс работ на одной захватке. 8.5 показаны изображения на сетевом графике поточных работ, однако при варианте «а» связи между работами 4-7 и 2-3 или 7-9 и 3-5, или 5-8 и 9-10 являются ложными и показывать их не следует. Введение в график дополнительных зависимостей 3-5, 6-9 и 10-12 (вариант «б») позволяет устранить эти ложные связи и правильно отразить фактические взаимозависимости работ при поточном их выполнении.
Поставки материалов, конструкций, оборудования, а также обеспечение стройки проектной документацией относятся к так называемым внешним работам и графически выделяются, например, утолщенной стрелкой с двойным кружком. Схемы нумерации (кодирования) событий графика 15. Нумерация или кодирование событий должны производиться в соответствии с последовательностью работ во времени, т. Предшествующим событиям должны присваиваться меньшие номера. Нумерацию событий целесообразно выполнять только после полного построения сети и производить от исходного события, которому присваивается нулевой или первый номер. Нельзя нумеровать последующее событие, если не пронумеровано предшествующее ему событие. Кодирование событий графика можно вести как по горизонтальной, так и по вертикальной схеме.
При горизонтальной схеме (см. 8.5, а) события кодируют слева направо по прямым до первого пересечения работ, а при вертикальной схеме (см. 8.5, 6) нумерацию начинают сверху вниз и снизу вверх с учетом того, чтобы каждое последующее событие получало номер после предыдущего. Укрупнение сетей. При разработке сетевых графиков на крупные объекты или комплексы для наглядности и лучшего контроля за ходом их строительства делают укрупнение сетей, т.
Группируют работы отдельных исполнителей или технологических комплексов, частей зданий (сооружений) и т. Так, работы сетевого графика можно укрупнить, представив отдельную группу работ одной работой, что упростит график. При укрупнении сетей нужно соблюдать следующие правила: группа работ может изображаться на сетевом графике как одна работа в том случае, если у этой группы одно начальное и одно конечное событие; укрупнять в одну работу следует только те из них, которые выполняются одним исполнителем (бригадой, участком и т. Д.), в укрупненную сеть нельзя вводить дополнительные события, которых нет в детализированных графиках; граничные события в детализированных и укрупненных графиках обязательно должны иметь одинаковые определения и один и тот же номер (код); наименование работ в укрупненном графике следует увязывать с наименованием укрупняемых работ; продолжительность укрупненной работы должна быть равна длине максимального пути укрупняемой группы детализированных работ; коды событий, которые сохраняются в укрупненном графике, должны быть такими же, как и в детализированном графике.
Довольно рациональным оказалось применение такой формы отображения строительного производственного процесса, как матрица, представляющая собой таблицу с пересекающимися строками и столбцами. На одной из строк матрицы выписываются виды работ, а на другой - захватки или частные фронты работ. В зависимости от того, какие показатели выписываются на ординате, матрицы строят в системе ОВР или ОФР (рис. В матрицах, построенных в системе ОВР, на оси ординат указывают виды работ, а на оси абсцисс - частные фронты, а в системе ОФР - наоборот.
Матрицы обычно составляют с использованием характеристик продолжительности работы или других показателей. Матрицы в системе ОФР (а) и ОВР (б) Представленные далее строительные потоки их виды и основные параметры матрицы могут использоваться для расчета потоков с непрерывным освоением ресурсов и фронтов работ, расчета потоков с критическими работами, при этом матричный расчет позволяет трансформировать его в линейный график, сетевой график и в циклограмму, т. Е., комбинируя различные формы моделей, можно получить легко изменяющуюся форму модели в зависимости от условий изменения внешних условий: финансирования, поставки материалов, дефицита квалифицированных рабочих кадров и т. Представление исходных данных для формирования расчета и оптимизации расписания работ в виде соответствующих матриц позволяет обеспечивать необходимую их детализацию.
При использовании матриц появляется возможность формирования различных вариантов организации работ и выбора из них более рационального, т. Обеспечения подлинно научной организации работ. К достоинствам матриц относится также четкость разграничения связей между работами.

Использование матриц в качестве модели организации работ позволяет определить такие важные расчетные показатели, как продолжительность влияния комплекса работ, ранние и поздние сроки их выполнения. Если пространство для отображения связей в матрице не ограничивать, а сами связи показывать стрелками, то она перерастает в сетевой график. Таким образом, матрицу можно рассматривать в качестве своеобразного нового метода имитационного моделирования календарных планов. На матричных моделях удается лучшим образом представить расстановку бригад по фронтам, добиться хорошей алгоритмизации расчета планов работ при самых разнообразных ограничениях, что позволяет составить и рассчитать большое количество вариантов организации выполнения комплекса работ. При разработке календарных планов могут быть использованы различные их формы, в том числе и вышеописанные (см.
Однако наиболее приемлемой для многих случаев организации работ является линейная модель в форме календарного плана.
Сетевой График Строительства Пример
Содержание. Представим себе ситуацию развития проекта капитального строительства на производственном предприятии. Проект успешно инициирован и полным ходом идут работы по его планированию.
Сформирована и утверждена, план по вехам принят. Разработан первичный вариант календарного плана. Поскольку задача оказалась достаточно масштабной, куратор принял решение о разработке еще и сетевой модели. Расчет сетевого графика в прикладном аспекте его исполнения является предметом настоящей статьи. Перед стартом моделирования Методологический базис сетевого проектного планирования представлен на нашем сайте несколькими статьями.
Я лишь сошлюсь на две из них. Это материалы, посвященные в целом и непосредственно. Если в ходе повествования у вас будут возникать вопросы, просмотрите ранее представленные осмысления, основная суть методологии в них изложена. В настоящей статье мы рассмотрим небольшой пример локальной части комплекса строительно-монтажных работ в рамках значительной проектной реализации.
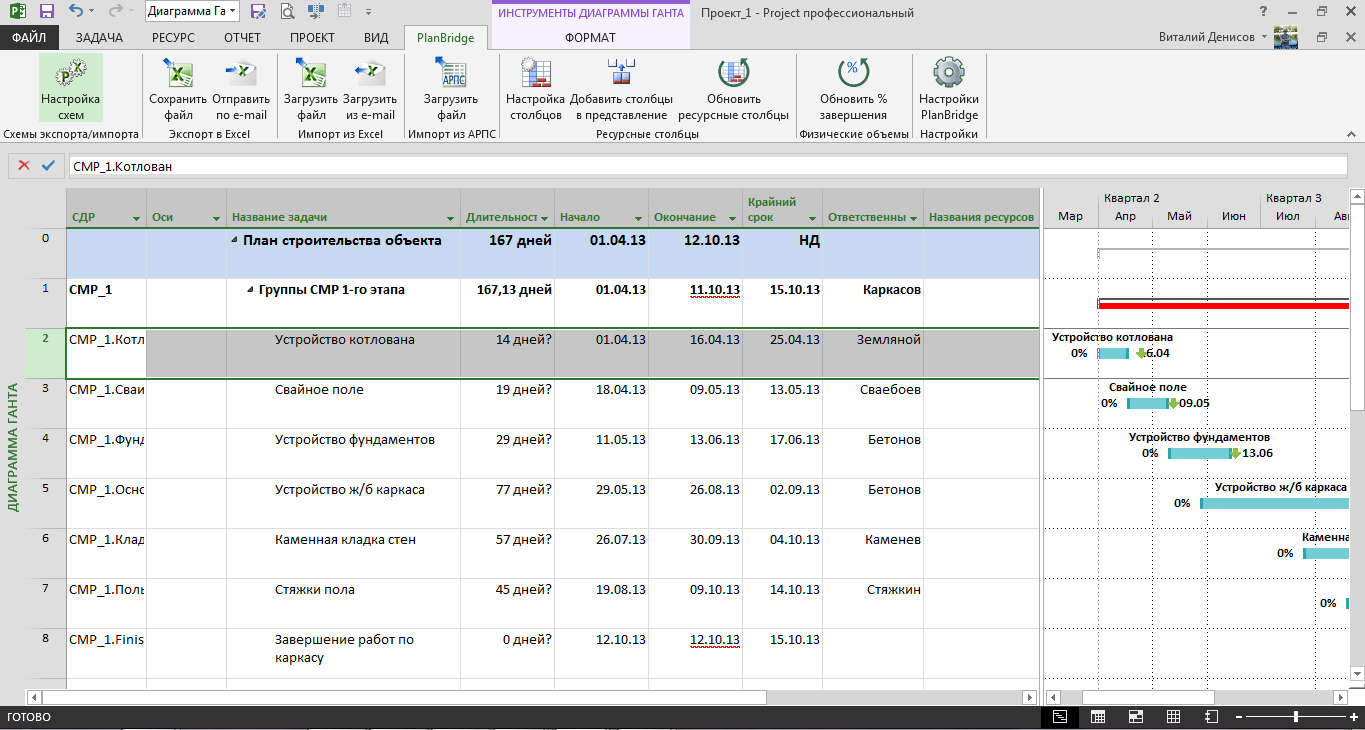
Расчеты и моделирование будем выполнять методом «вершина-работа» и классическим табличным способом («вершина-событие») с применением МКР (метода критического пути). Построение сетевого графика мы начнем на основе первой итерации календарного плана, выполненного в форме диаграммы Ганта. Для целей наглядности предлагаю не учитывать отношения предшествования и максимально упростить последовательность действий. Хотя на практике такое бывает редко, представим в нашем примере, что операции выстроены в последовательность вида «окончание-начало». Ниже вашему вниманию представляются две таблицы: выписка из списка работ проекта (фрагмент из 15-ти операций) и список параметров сетевой модели, необходимый для представления формул. Формулы расчета параметров сетевого графика Что нам потребуется определить в ходе построения графика?.
Раннее начало текущей работы, в которую входят несколько связей от предыдущих операций. Выбираем максимальное значение из всех ранних окончаний предыдущих операций. Позднее окончание текущего действия, из которого выходят несколько связей. Выбираем минимальное значение из всех поздних начал последующих действий. Последовательность работ, формирующих критический путь. У этих действий раннее и позднее начала равны, как и раннее и позднее окончание соответственно. Резерв такой операции равен 0.
Полные и частные резервы. Коэффициенты напряженности работ. Логику формул резервов и коэффициента напряженности работы мы рассмотрим в специальном разделе. Последовательность действий по моделированию Шаг первый Построение сетевого графика начинаем путем размещения прямоугольников задач последовательно слева-направо, применяя правила, описанные в предыдущих статьях. При выполнении моделирования методом «вершина-работа» основным элементом диаграммы выступает семисегментный прямоугольник, в составе которого отражены параметры начала, окончания, длительности, резерва времени и наименования или номера операций. Схема представления ее параметров показана далее.
Результат первого этапа построения сетевого графика В соответствии с логикой последовательности операций с помощью специализированной программы, MS Visio или любого редактора размещаем образы работ в заданном выше формате. В первую очередь заполняем наименования выполняемых действий, их номера и длительность.
Рассчитываем раннее начало и раннее окончание с учетом формулы раннего начала текущего действия в условиях нескольких входящих связей. И так проходим до завершающей фрагмент операции. При этом, в нашем примере проекта тем же графиком Ганта не предусмотрены исходящие связи от операций 11, 12, 13 и 14. «Подвешивать» их на сетевой модели недопустимо, поэтому мы добавляем фиктивные связи к конечной работе фрагмента, выделенные на рисунке синим цветом. Шаг второй Находим критический путь. Как известно, это путь, имеющий самую большую продолжительность действий, которые в него входят.
Просматривая модель, мы выбираем связи между работами, имеющими максимальные значения раннего окончания действий. Намеченный критический путь выделяем стрелочками красного цвета. Полученный результат представлен на промежуточной схеме далее. Схема сетевого графика с выделенным критическим путем Шаг третий Заполняем значения позднего окончания, позднего начала и полного резерва работ. Для выполнения расчета переходим к конечной работе и берем ее за последнюю операцию критического пути. Это означает, что поздние значения окончания и начала идентичны ранним, и от последней операции фрагмента мы начинаем двигаться в обратную сторону, заполняя нижнюю строку схематического представления действия. Модель выполнения расчета показана ниже на схеме.
Итоговый вид сетевого графика Шаг четвертый Четвертым шагом алгоритма сетевого моделирования и расчетов выполняется вычисление резервов и коэффициента напряженности. Первым делом имеет смысл обратить внимание на полные резервы путей некритических направлений (R). Они определяются путем вычитания из продолжительности критического пути временной длительности каждого из этих путей, пронумерованных на схеме итогового сетевого графика. R пути под номером 1 = 120 – 101 = 19;.
R пути под номером 2 = 120 – 84 = 36;. R пути под номером 3 = 120 – 104 = 16;. R пути под номером 4 = 120 – 115 = 5;. R пути под номером 5 = 120 – 118 = 2;.
R пути под номером 6 = 120 – 115 = 5. Дополнительные расчеты модели Выполнение расчета общего резерва текущей операции производится путем вычитания из значения позднего начала раннего начала или из позднего окончания раннего окончания (см. Схему расчета выше). Общий (полный) резерв показывает нам возможность начала текущей работы позже или увеличения продолжительности на длительность резерва. Но нужно понимать, что пользоваться полным резервом следует с большой осторожностью, потому что работы, стоящие от текущего события дальше остальных, могут оказаться без запаса времени.
Помимо полных резервов в сетевом моделировании оперируют также и частными или свободными резервами, которые представляют собой разницу между ранним началом последующей работы и ранним окончанием текущей. Частный резерв показывает, есть ли возможность сдвинуть ранее начало операции вперед без ущерба для начала следующей процедуры и всему графику в целом. Следует помнить, что сумма всех частных резервных значений тождественна полному значению резерва для рассматриваемого пути. Главной задачей выполнения вычислений различных параметров является оптимизация сетевого графика и оценка вероятности выполнения проекта в срок. Одним из таких параметров является коэффициент напряженности, который показывает нам уровень сложности реализовать работу в намеченный срок.
Формула коэффициента представлена выше в составе всех расчетных выражений, применяемых для анализа сетевого графика. Коэффициент напряженности определяется как разница между единицей и частного от деления полного резерва времени работы на разницу длительности критического пути и особого расчетного значения. Это значение включает ряд отрезков критического пути, совпадающих с максимально возможным путем, к которому может быть отнесена текущая операция (i-j). Далее помещен расчет частных резервов и коэффициентов напряженности работ для нашего примера.
Таблица расчета частных резервов и коэффициента напряженности Коэффициент напряженности варьируется от 0 до 1,0. Значение 1,0 устанавливается для работ, находящихся на критическом пути. Чем ближе значение некритической операции к 1,0, тем труднее удержаться в плановых сроках ее реализации. После того, как значения коэффициента по всем действиям графика посчитаны, операции, в зависимости от уровня этого параметра, могут быть отнесены к категории:. критической зоны (Кн более 0,8);. подкретической зоны (Кн более или равно 0,6, но менее или равно 0,8);.
резервной зоны (Кн менее 0,6). Оптимизация сетевой модели, нацеленная на сокращение общей продолжительности проекта, как правило, обеспечивается следующими мероприятиями. Перераспределение ресурсов в пользу наиболее напряженных процедур. Снижение трудоемкости операций, расположенных на критическом пути. Распараллеливание работ критического пути. Переработка структуры сети и состава операций. Использование табличного метода Общепризнанные ПП календарного планирования (MS Project, Primavera Suretrack, OpenPlan и т.п.) способны вычислять ключевые параметры сетевой модели проекта.
Мы же в настоящем разделе табличным методом выполним настройку подобного расчета обычными средствами MS Excel. Для этого возьмем наш пример фрагмента проектных операций проекта в области СМР. Расположим основные параметры сетевого графика в столбах электронной таблицы. Модель расчета параметров сетевого графика табличным способом Преимуществом выполнения расчетов табличным способом является возможность простой автоматизации вычислений и избежание массы ошибок, связанных с человеческим фактором.
Красным цветом будем выделять номера операций, располагающихся на критическом пути, а синим цветом отметим расчетные позиции частных резервов, превышающих нулевое значение. Разберем пошагово расчет параметров сетевого графика по основным позициям. Ранние начала операций, следующих за текущей работой. Алгоритм расчета настраиваем на выбор максимального значения из раннего времени окончания нескольких альтернативных предыдущих действий. Взять, например, операцию под номером 13. Ей предшествуют работы 6, 7, 8.
Из трех ранних окончаний (71, 76, 74 соответственно) нам нужно выбрать максимальное значение – 76 и проставить его в качестве раннего начала операции 13. Критический путь.
Выполняя процедуру расчета по пункту 1 алгоритма, мы доходим до конца фрагмента, найдя значение продолжительности критического пути, которая в нашем примере составила 120 дней. Значения наибольших ранних окончаний среди альтернативных действий обозначают операции, лежащие на критическом пути. Отмечаем эти операции красным цветом. Поздние окончания операций, предшествующих текущей работе. Начиная с концевой работы начинаем движение в обратную сторону от действий с большими номерами к операциям с меньшими.
При этом из нескольких альтернатив исходящих работ выбираем наименьшее знание позднего начала. Поздние начала вычисляем как разницу между выбранными значениями поздних окончаний и продолжительности операций. Резервы операций. Вычисляем полные (общие) резервы как разницу между поздними началами и ранними началами либо между поздними окончаниями и ранними окончаниями. Значения частных (свободных) резервов получаем в результате вычитания из числа раннего начала следующей операции раннего окончания текущей. Мы рассмотрели практические механизмы составления сетевого графика и расчета основных параметров временной продолжительности проекта.
Сетевой График Строительства Жилого Дома Пример
Таким образом, вплотную приблизились к исследованию возможностей анализа, проводимого с целью оптимизации сетевой модели и формирования непосредственно плана действий по улучшению ее качества. Настоящая тема занимает немного места в комплексе знаний проект-менеджера и не так уж и сложна для восприятия.
Во всяком случае, каждый РМ обязан уметь воспроизводить визуализацию графика и выполнять сопутствующие расчеты на хорошем профессиональном уровне.





